Bassregler für Tele, Strat und Les Paul – beschrieben von Jon Blackstone und hier diskutiert: Nach der Theorie: Telecaster – ein Draht wird umgesteckt; Stratocaster – ein zweifacher Bassregler und Les Paul – der Bassregler wird umgeschaltet. Am Ende noch ein Einhand-Radioknopf.
Bass-Ton-Regler für Gitarren
Kapitelinhalt:[ Überspringen ]- Theorie, Theorie, Theorie •
- Telecaster – Bass- statt Höhenregler •
- Stratocaster – zwei Klangregler •
- Les Paul – umschaltbarer Klangregler •
- P. S: Les Paul – doppelter Klangregler •
- Fazit
Theorie, Theorie, Theorie
Vor längerer Zeit fand der Autor auf der Seite von Jon Blackstone einen Artikel “Teach Your Neck Pickup to Twang” – über die mögliche Verwendung eines Bassreglers für den Halstonabnehmer einer Gitarre (Telecaster, Stratocaster, Les Paul), um einen für die fünfziger Jahre typischen Klang zu erzielen.
Im Folgenden sollen diese Vorschläge diskutiert werden. Dazu werden die Schaltungen als Schaltpläne (nicht als Verkabelungspläne) wieder neu gezeichnet, Gegenvorschläge erläutert und – für eine vereinfachte Schaltung – die Knickfrequenzen bzw. die sogenannten −3dB-Frequenzen und das maximale Maß der Dämpfung berechnet.
Die stark vereinfachte Bassregler-Schaltung wird in der folgenden Abbildung 6.1 gezeigt – links zu Berechnung abstrahiert und rechts in der von Jon Blackstone vorgeschlagenen Anwendung:

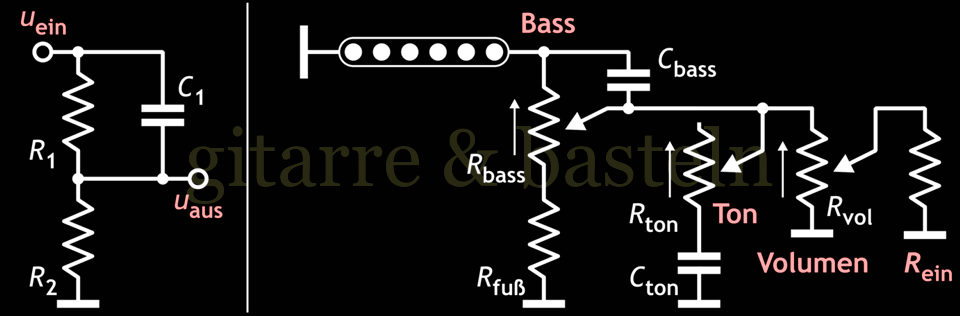
Abb. 6.1: Schaltungsprinzip für einen Bassregler in einer Gitarre – links: allgemeines Prinzip zur Ableitung der Frequenzen; rechts: Schaltung mit mehreren bereits vorhandenen Widerständen.
Die Schaltungen lassen sich also auf die in Abbildung 6.1 links gezeigte Grundschaltung und deren Frequenzgang auf die folgende Gleichung 6.1 hin abstrahieren:
\( \begin{eqnarray} \frac{u_{\textrm{aus}}}{u_{\textrm{Ein}}} & = & \frac{R_{2} } {R_{2} + (R_{1}\,||\,X_{C1}) } \\~\\ & = & \frac{R_{2} } {R_{2} + \cfrac {R_{1} \cdot{} X_{C1}} {R_{1} + X_{C1}} } \\~\\ & = & \frac{R_{2} } {R_{2} + \cfrac {R_{1} \cdot{} \cfrac{1}{ȷωC_{1}}} {R_{1} + \cfrac{1}{ȷωC_{1}}} } \\~\\ & = & \frac{R_{2} } {R_{2} + \cfrac {R_{1}} {R_{1} \cdot{} ȷωC_{1} + 1} } \\~\\ & = & \frac{R_{2} \cdot{}\! \left( R_{1} \cdot{} ȷωC_{1} + 1 \right) } {R_{2} \cdot{}\! \left( R_{1} \cdot{} ȷωC_{1} + 1 \right) + R_{1} } \\~\\ & = & \frac{ R_{1}R_{2} \cdot{} ȷωC_{1} + R_{2} } { R_{1}R_{2} \cdot{} ȷωC_{1} + R_{1} + R_{2} } \\~\\ & = & \frac{R_2} {R_1 + R_2} \cdot{}\! \frac{ R_{1} \cdot{} ȷωC_{1} + 1 } {\cfrac{R_{1}\cdot{R_{2}}} { R_{1} + R_{2} } \cdot{} ȷωC_{1} + 1 } \\~\\ \frac{u_{\textrm{aus}}}{u_{\textrm{Ein}}} & = & \frac{R_2} {R_1 + R_2} \cdot{}\! \frac{ ȷωC_{1}R_{1} + 1 } { ȷωC_{1} \left( R_{1}\,||\,R_{2} \right) + 1 } \tag{6.1}\end{eqnarray} \)
Aus dieser Gleichung ergeben sich zwei −3dB-Frequenzen – f1 und f2:
\( \begin{eqnarray} f_1 & = & \frac{1} { 2π\cdot{}C_{1}\cdot{}R_{1} } \\~\\ f_2 & = & \frac{1} { 2π\cdot{}C_{1}\cdot{}\! \left( R_{1}\,||\,R_{2} \right) } \tag{6.2}\end{eqnarray} \)
und eine maximale Dämpfung Dmax:
\( \begin{eqnarray} D_{max} [\textrm{dB}] & = & 20\cdot{}\! \log \left( \frac{f_2} {f_1} \right) \\~\\ & = & 20\cdot{}\! \log \left( \frac{R_1} {R_1\,||\,R_2} \right) \\~\\ & = & 20\cdot{}\! \log \left( \frac{R_1\cdot{}(R_1 + R_2)} {R_1\cdot{}R_2} \right) \\~\\ & = & 20\cdot{}\! \log \left( \frac{R_1} {R_2} + 1 \right) \tag{6.3}\end{eqnarray} \)
Es gibt also eine Maximaldämpfung insbesondere für die tiefen Frequenzen, die vom Verhältnis der beiden Widerstände R1 zu R2 bzw. vom Verhältnis der beiden −3dB-Frequenzen f1 zu f2 abhängt. Mit der Veränderung des Kondensators C1 werden beide Frequenzen nach unten oder oben verschoben, ohne dass sich die Dämpfung und die Form der Dämpfungskurve ändern.
Mit der in Abbildung 6.1 rechts gezeigten Schaltung werden die Verhältnisse insofern komplizierter, als das sich unterer und oberer Widerstand mit der Stellung des Bassreglers verändern. Für eine einfachere Betrachtung wird von der maximalen Bassdämpfung (Schleifer des Bassreglers an der Verbindung zwischen Rbass und Rfuß) ausgegangen.
In diesem Fall bilden die Widerstände Rfuss (bei einer Stratocaster vielleicht 150 kΩ), RTon (220 kΩ; CTon spielt bei voll aufgedrehtem Tonregler keine Rolle, die −3dB-Frequenz von RTon und CTon liegt bei etwa 15 Hz), der Volumenregler RVol (220 kΩ;) und der Eingangswiderstand der folgenden Stufe (1 MΩ) den unteren Widerstand R2 mit etwa 60 kΩ.
Es sollte auch klar sein, dass die Stellung des Tonreglers (wenn der Tonregler hinter dem Bassregler liegt) die maximale Bassabsenkung über die beschriebene Parallelschaltung mit beeinflusst – je weiter der Tonregler „hinter“ dem Bassregler zurückgedreht wird, desto stärker ist auch die maximale Bassabsenkung.
Soweit die Theorie vorweg, nun zu den Vorschlägen für die einzelnen Gitarren:
Telecaster – Bass- statt Höhenregler
Zunächst die von Jon Blackstone vorgeschlagene Schaltung für die Telecaster – hier aus Gründen des Urheberrechts wie der besseren Übersicht zuliebe ein eigens erstellter Schaltplan und kein Verdrahtungsplan:
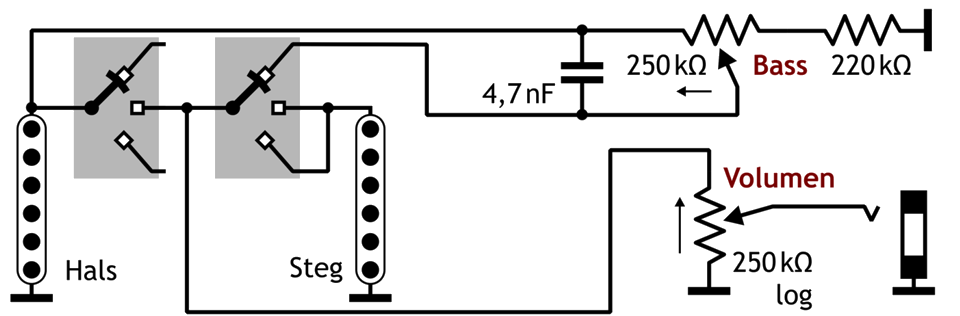
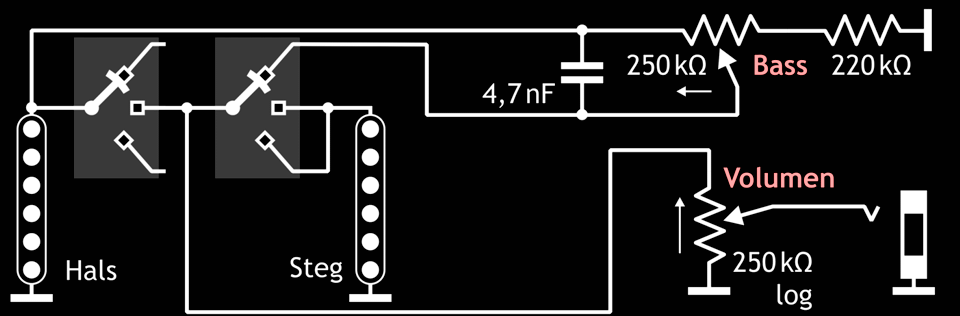
Abb. 6.2: Schaltungsvorschlag von Jon Blackstone für eine regelbare Basssperre in einer Telecaster (Schalter auf Stellung Halstonabnehmer).
Man sieht, dass die Tonabnehmer in der Mittelstellung des Schalters immer noch mit der Bassregler-Schaltung belastet werden, was möglicherweise die Höhenwiedergabe ungünstig beeinflussen kann.
Sinnvoller kann es sein, das Kabel vom Hals-Tonabnehmer nicht direkt mit dem oberen Ende des Bassreglers zu verbinden, sondern, wie in der folgenden Abbildung 6.3 gezeigt, über den Schalter zu gehen:
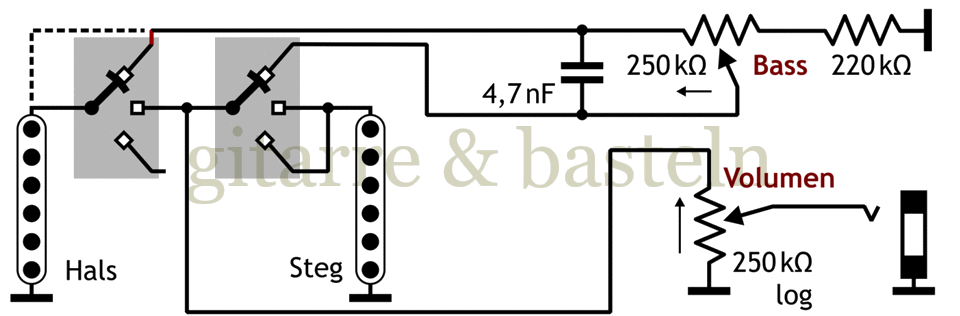
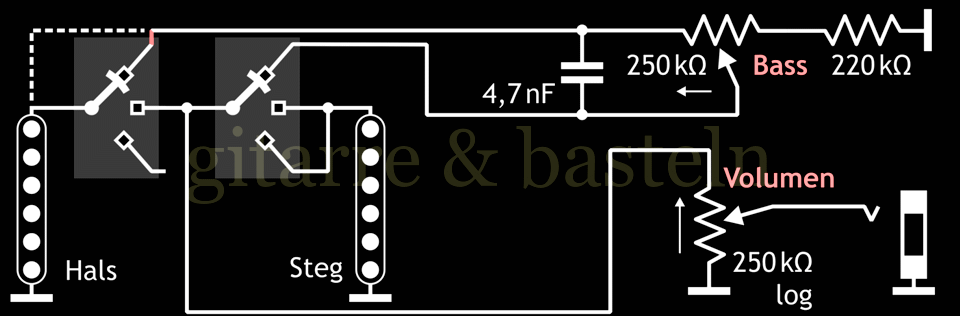
Abb. 6.3: Schaltungsvorschlag von Jon Blackstone für eine regelbare Basssperre in einer Telecaster mit Änderungsvorschlag durch den Autor – anstelle der gestrichelt die rot gezeichnete Verbindung (Schalter auf Stellung Halstonabnehmer).
Die beiden −3dB-Frequenzen für den Frequenzgang der Bassabsenkung in einer Schaltung entsprechend Abbildung 6.3 ergeben sich zu:
\( \begin{eqnarray} f_1 & = & \frac{1} { 2π\cdot{}C_{Bass}\cdot{}R_{Bass} } \\~\\ & = & \frac{1} {2π\cdot{} 0{,}0047\,\textrm{μF}\cdot{} 0{,}25\,\textrm{MΩ} } \\~\\ & = & \frac{1} {2π\cdot{} 0{,}0047\cdot{}0{,}25 } \cdot{}\! \frac{1} {10^{-6}\cdot{} 10^{6}} \cdot{}\! \frac{\mathrm{V}\cdot{} \mathrm{A} } {\mathrm{As}\cdot{} \mathrm{V} } \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}0047\cdot{}0{,}25 } \\~\\ f_1 & \approx{} & 135\,\textrm{Hz} \tag{6.4}\end{eqnarray} \)
Für f2 wird die Umstellerei von eins durch Microfarad und eins durch Megaohm zu Hertz übersprungen:
\( \begin{eqnarray} f_2 & = & \frac{1} { 2π\cdot{}C_{Bass}\cdot{}\! \left( R_{Bass}\,||\,R_{Fuß}\,||\,R_{Vol} \right) } \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}0047\cdot{}\! \left( 0{,}25\,||\,0{,}22\,||\,0{,}25 \right)} \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}0047\cdot{}0{,}08 } \\~\\ f_2 & \approx{} & 420\,\textrm{Hz} \tag{6.5}\end{eqnarray} \)
Für die maximale Bassabsenkung lässt sich ableiten:
\( \begin{eqnarray} D_{max} [\textrm{dB}] & = & 20\cdot{}\! \log \left( \frac{f_2} {f_1} \right) \\~\\ & = & 20\cdot{}\! \log \left( \frac{420\,\textrm{Hz}} {135\,\textrm{Hz}} \right) \\~\\ D_{max} & \approx & 10\,\textrm{dB} \tag{6.6}\end{eqnarray} \)
Stratocaster – zwei Klangregler
Auch für die Stratocaster gibt es auf der Seite von Jon Blackstone einen Schaltungsvorschlag – einer der beiden Tonregler wird zum Bassregler für den einzelnen Halstonabnehmer, der andere zum allgemeinen Tonregler (Höhenblende):
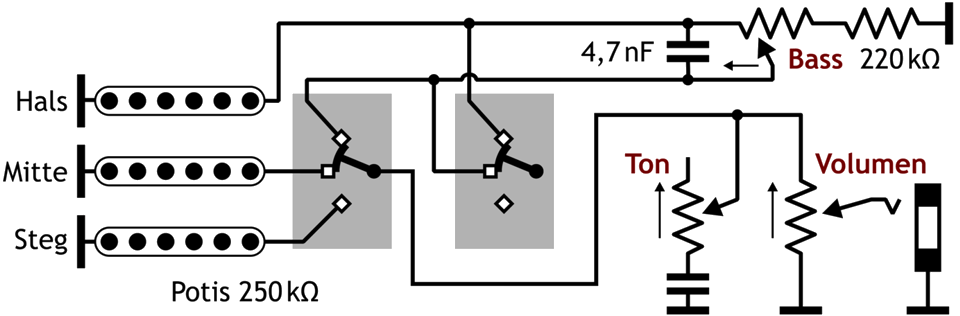
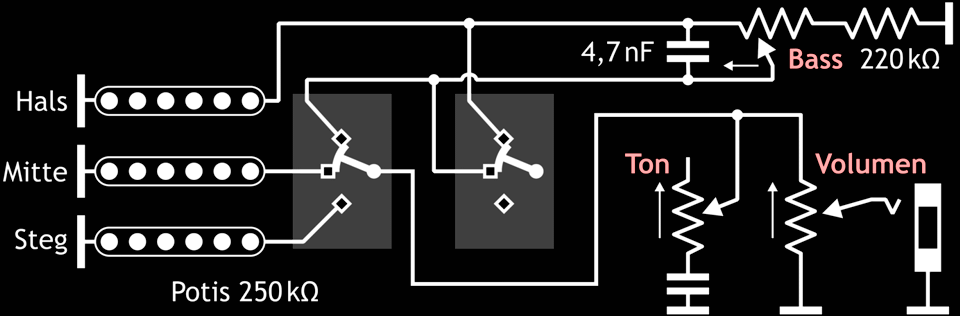
Abb. 6.4: Schaltungsvorschlag von Jon Blackstone für eine regelbare Basssperre in einer Stratocaster (Schalter auf Stellung Hals- und Mitteltonabnehmer).
Der Frequenzgang der Schaltung verändert sich ein wenig dadurch, dass hinter dem Bassregler noch ein Tonregler liegt. Zunächst wird also gerechnet. Die tiefste untere −3dB-Frequenz ist hier gleich geblieben:
\( \begin{eqnarray} f_1 & = & \frac{1} { 2π\cdot{}C_{Bass}\cdot{}R_{Bass} } \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}0047\cdot{}0{,}25 } \\~\\ f_1 & \approx{} & 135\,\textrm{Hz} \tag{6.7}\end{eqnarray} \)
Durch den hinter dem Bassregler zugeschalteten Tonregler verringert sich der untere Widerstand, der Gesamtwiderstand der Parallelschaltung und es erhöht sich die obere −3dB-Frequenz:
\( \begin{eqnarray} f_2 & = & \frac{1}{2π\cdot{} C_{Bass}}\cdot{} \\&& \frac{1} { \left( R_{Bass}\,||\,R_{Fuss}\,||\,R_{Ton}\,||\,R_{Vol}\,||\,R_{Ein} \right) } \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}0047}\cdot{} \\&& \frac{1} {\left( 0{,}25\,||\,0{,}22\,||\,0{,}25\,||\,0{,}25 \,||\,1 \right)} \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}0047\cdot{}0{,}059 } \\~\\ f_2 & \approx{} & 570\,\textrm{Hz} \tag{6.8}\end{eqnarray} \)
Mit der Erhöhung von f2 erhöht sich auch die maximale Bassabsenkung:
\( \begin{eqnarray} D_{max} [\textrm{dB}] & = & 20\cdot{}\! \log \left( \frac{f_2} {f_1} \right) \\~\\ & = & 20\cdot{}\! \log \left( \frac{570\,\textrm{Hz}} {135\,\textrm{Hz}} \right) \\~\\ D_{max} & \approx & 13\,\textrm{dB} \tag{6.9}\end{eqnarray} \)
Allerdings finden sich hier zwei kleine Nachteile:
-
Zum einen belastet der Bassregler auch in der Zwischenposition Hals- und Mitteltonabnehmer die Tonabnehmer bzw. deren Höhenwiedergabe.
-
Zum anderen könnte der Tonregler den Bassregler beeinflussen, da er hinter dem Bassregler liegt.
Aus diesem Grunde wird eine Schaltung vorgeschlagen, bei der – bei einem „größeren“ Bassregler – auf den Fußwiderstand verzichtet wird. Weiterhin wird die Verwendung eines eher speziellen „MN“-Potentiometers von Bourns vorgeschlagen, mit dem man nicht nur einen Bassregler nur für den Halstonabnehmer realisieren kann, sondern auch noch einen für alle Tonabnehmer.
Beschreibung des MN-Potentiometers:
Dieses MNTandem-Potentiometer (genauer gesagt, das “Bourns® Model PDB182-GTRB Blend-Balance Guitar Potentiometer” – Dokumentation siehe diese PDF, Bezug z. B. über musikding.de) dient eigentlich dazu, die Signale zweier Tonabnehmer zu mischen – d. h. eine Drehung von der Mitte nach rechts regelt den ersten Tonabnehmer herunter (und verändert den zweiten überhaupt nicht), Drehung von der Mitte nach links verändert den ersten Tonabnehmer überhaupt nicht (und regelt den zweiten herunter).
Die folgende Abbildung 6.5 – ein Faksimile aus den Herstellerinformationen – zeigt das Verhalten des MN-Potentiometers noch einmal in einem Diagramm.

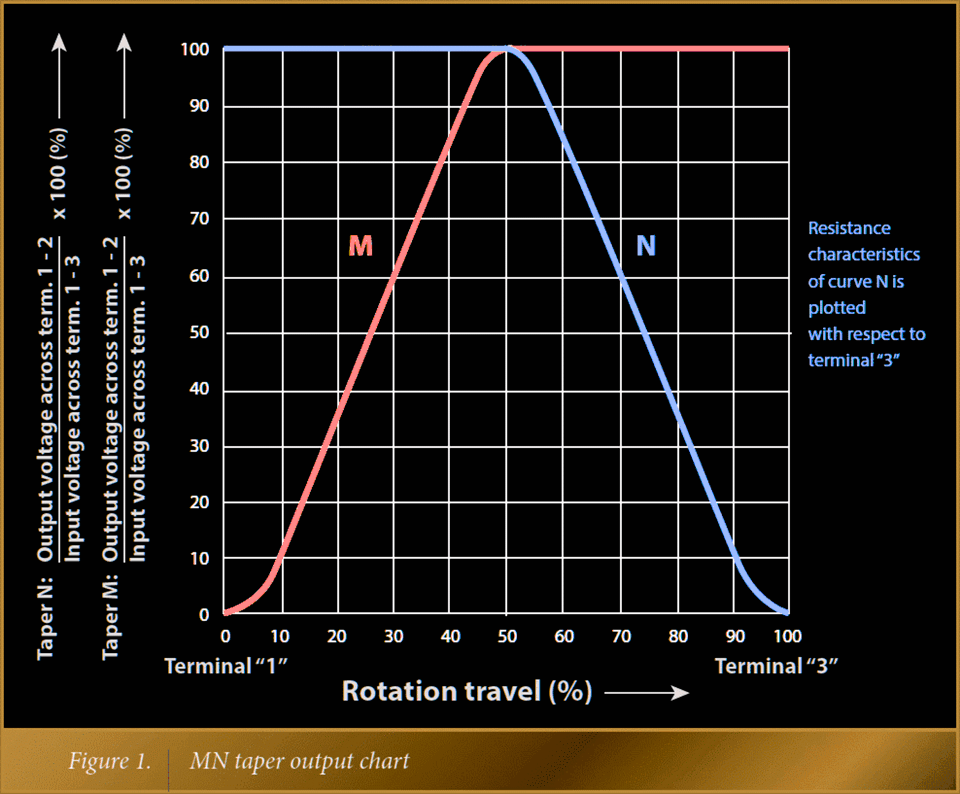
Abb. 6.5: Regelcharakteristik eines MN-Potentiometers – Faksimile aus den Herstellerinformationen.
Das heißt, eines der beiden einzelnen Potentiometer des Tandempotentiometers funktioniert nur „links von der Mitte“, das andere nur „rechts davon“.
Mit diesem „MN“-Potentiometer ist ein „doppelter“ Bassregler möglich – entweder – von der Mitte nach links gedreht – ein Bassregler nur für den Hals-Tonabnehmer allein oder – von der Mitte nach rechts gedreht – ein Bassregler für alle Tonabnehmerkombinationen. Der Bassregler für den Halstonabnehmer wird in allen anderen Tonabnehmerkombinationen vom 5-Positions-Schalter kurzgeschlossen.
Der Höhenregler für alle Tonabnehmer liegt dabei vor dem Bassregler, kann diesen also schwerer beeinflussen;
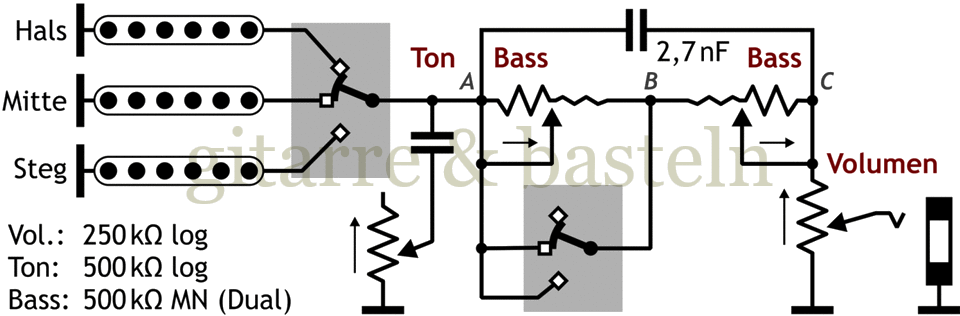
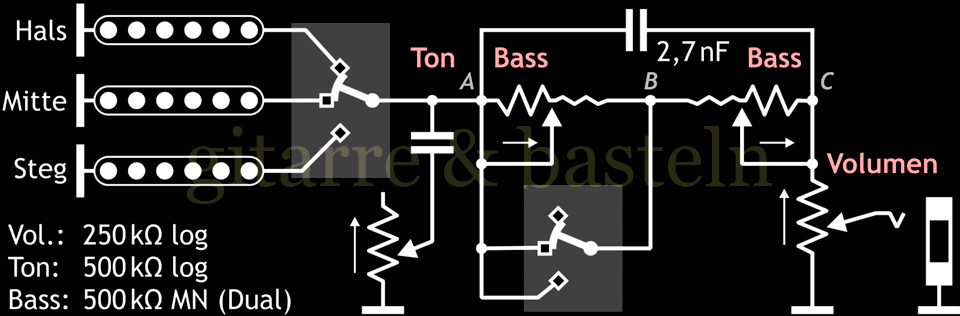
Abb. 6.6: Schaltungsvorschlag mit einem regelbaren Lowcut für den Halstonabnehmer oder alle Tonabnehmer in einer Stratocaster mittels eines MN-Potentiometers (Schalter auf Stellung Hals- und Mitteltonabnehmer).
Zur Simulation des Frequenzganges der vorgeschlagenen Schaltung siehe die folgende Abbildung 6.7 – mit dem Eingangswiderstand von 1 MΩ ist der des nachfolgenden Verstärkers gemeint, mit dem Bassregler 480 kΩ das MN-Potentiometer (wie gemessen):
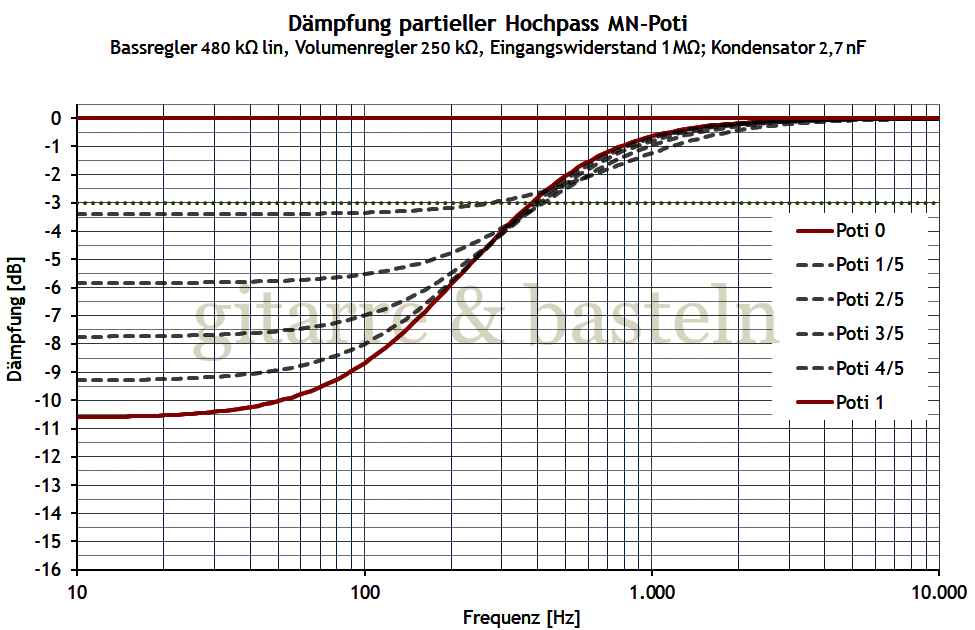
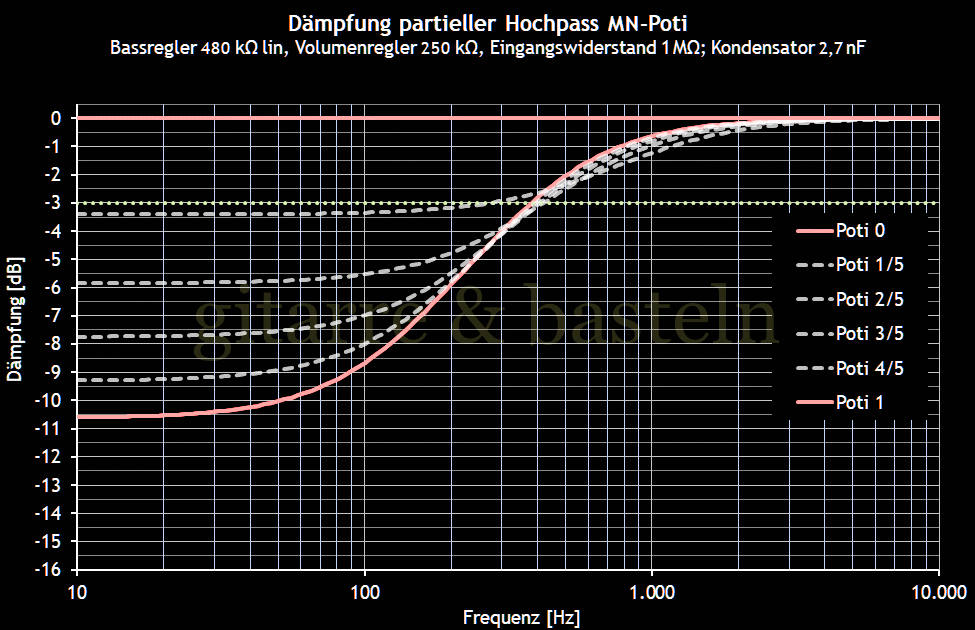
Abb. 6.7: Frequenzgänge für ein doppeltes Bassfilter in einer Stratocaster-Gitarre – Schaltung entsprechend Abbildung 6.6.
Dazu noch die passende Herleitung. Der Kondensator wird von 4,7 nF auf 2,7 nF verkleinert, um mit dem größeren Bassregler auf eine ähnliche untere −3dB-Frequenz zu kommen:
\( \begin{eqnarray} f_1 & = & \frac{1} { 2π\cdot{}C_{Bass}\cdot{}R_{Bass} } \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}0027\cdot{}0{,}48 } \\~\\ f_1 & \approx{} & 120\,\textrm{Hz} \tag{6.10}\end{eqnarray} \)
f2 ist trotzdem ein wenig kleiner:
\( \begin{eqnarray} f_2 & = & \frac{1} { 2π\cdot{}C_{Bass}\cdot{}% \left(% R_{Bass}\,||\,R_{Vol}\,||\,R_{Ein} \right) } \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}0027\cdot{}\! \left( 0{,}48\,||\,0{,}25 \,||\,1 \right)} \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}0027\cdot{}0{,}14 } \\~\\ f_2 & \approx{} & 420\,\textrm{Hz} \tag{6.11}\end{eqnarray} \)
wodurch auch die Dämpfung im Bass geringer ist:
\( \begin{eqnarray} D_{max} [\textrm{dB}] & = & 20\cdot{}\! \log \left( \frac{f_2} {f_1} \right) \\~\\ & = & 20\cdot{}\! \log \left( \frac{420\,\textrm{Hz}} {120\,\textrm{Hz}} \right) \\~\\ D_{max} & \approx & 11\,\textrm{dB} \tag{6.12}\end{eqnarray} \)
Die mögliche maximale Bassdämpfung ergibt sich zu etwa 11 dB. Letztendlich führt hier der fehlende zusätzliche Fußwiderstand zu einem kleineren Wert von f2 und zu einer geringeren maximalen Bassdämpfung.
Zwei Nachteile des Schaltungsvorschlags sollen nicht verschwiegen werden – es gibt keinen zusätzlichen Fußwiderstand des Bassspannungsteilers und der Vorwiderstand ist relativ klein. Ersteres macht die Schaltung relativ empfindlich für die Auswirkung eines kleineren Eingangswiderstands im ersten nachfolgenden Effektgerät oder Verstärker, während letzteres die mögliche maximale Absenkung begrenzt.
Das erste Problem kann man mit einem festen ersten nachfolgenden Gerät mit einem hohen Eingangswiderstand umgehen – ein Eingangspuffer auf dem Pedalboard, Stimmgerät etc. könnten helfen. Das zweite Problem (der zu geringe maximale Vorwiderstand) ließe sich mit einem MN-Potentiometer 1 MΩ lösen – dieses würde einen größeren Regelumfang bieten; der Autor hat ein solches beim Anbieter musikding.de nicht gefunden. Ein größerer Wert für das MN-Potentiometer verlangt aber möglicherweise einen kleineren Wert für den Kondensator.
Ein Kompromiss könnte darin bestehen, den Tonregler zwischen die beiden einzelnen Potentiometer des MN-Potentiometers zu legen – für den Halstonabnehmer liegt der Bassregler vor dem Tonregler (größere Bassabsenkung, Tonregler beeinflusst Bassregler), für alle Tonabnehmer dahinter (geringere Bassabsenkung, Tonregler beeinflusst Bassregler nicht):

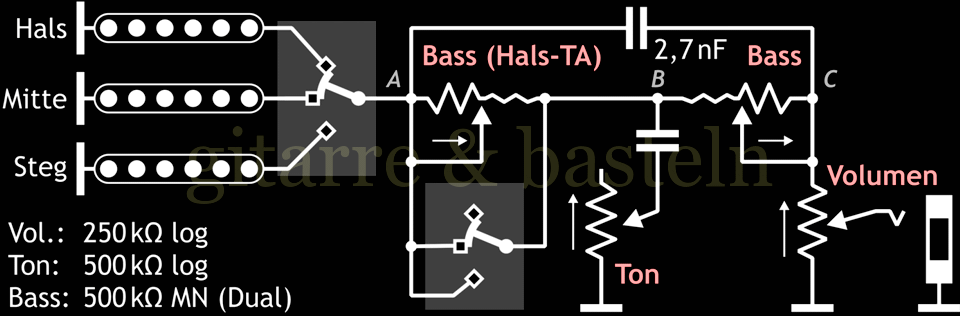
Abb. 6.8: Modifikation des Schaltungsvorschlags in Abbildung 6.6 einer regelbaren Basssperre – der Bassregler liegt für den Halstonabnehmer vor dem Tonregler (etwas größerer Regelumfang, aber mögliche Wechselwirkungen der beiden Regler).
Mit diesem Schaltungstrick kann die obere −3dB-Frequenz für den Halstonabnehmer und damit die maximale Bassdämpfung erhöht werden:
\( \begin{eqnarray} f_2 & = & \frac{1} { 2π\cdot{}C_{Bass}\cdot{}\! \left( R_{Bass}\,||\,R_{Treble}\,||\,R_{Vol}\,||\,R_{Ein} \right) } \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}0027\cdot{}\! \left( 0{,}48\,||\,0{,}48\,||\,0{,}25 \,||\,1 \right)} \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}0027\cdot{}0{,}11 } \\~\\ f_2 & \approx{} & 540\,\textrm{Hz} \tag{6.13}\end{eqnarray} \)
Für die maximale Dämpfung im Bass ergibt sich jetzt:
\( \begin{eqnarray} D_{max} [\textrm{dB}] & = & 20\cdot{}\! \log \left( \frac{f_2} {f_1} \right) \\~\\ & = & 20\cdot{}\! \log \left( \frac{540\,\textrm{Hz}} {120\,\textrm{Hz}} \right) \\~\\ D_{max} & \approx & 13\,\textrm{dB} \tag{6.14}\end{eqnarray} \)
Unabhängig davon könnte auch noch der Kondensator über dem Bassregler „aufgeteilt“ werden – einmal zwischen den Punkten A und B für den Bassregler des Halstonabnehmers bzw. einmal zwischen den Punkten B und C für den Bassregler aller Tonabnehmer, was die Möglichkeit eröffnet, beide Kondensatoren jeweils in der Größe klanglich anzupassen.
Les Paul – umschaltbarer Klangregler
Der Bassregler für den Hals-Tonabnehmer der Les Paul ist praktisch, es mag aber Anwendungen geben, für die man sogar dort eine Höhenblende braucht (extrem gediegener Jazz?, King-Crimson-Solos?). Deswegen sollte auch dieser Regler umschaltbar sein.
Zunächst erst einmal in der folgenden Abbildung 6.9 der Schaltungsvorschlag von Jon Blackstone – wieder in einem Schalt- statt Verdrahtungsplan:

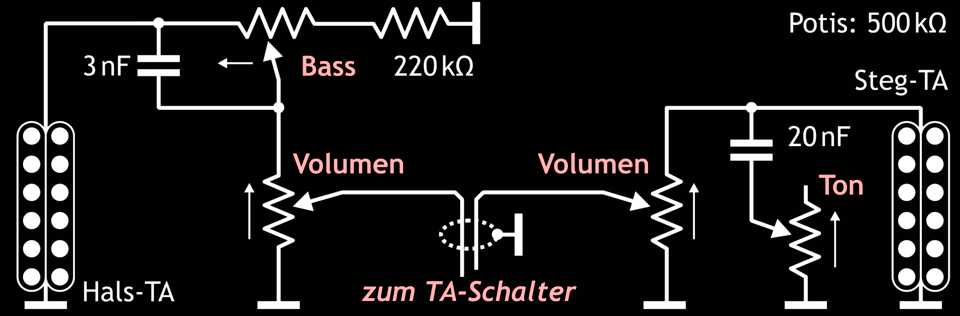
Abb. 6.9: Schaltungsvorschlag von Jon Blackstone für eine regelbare Basssperre in einer Les Paul.
Anschließend in Abbildung 6.10 der Schaltplan mit dem umschaltbaren Regler – hier genügt ein übliches Push-Pull-Potentiometer mit einem zweipoligen Umschalter:

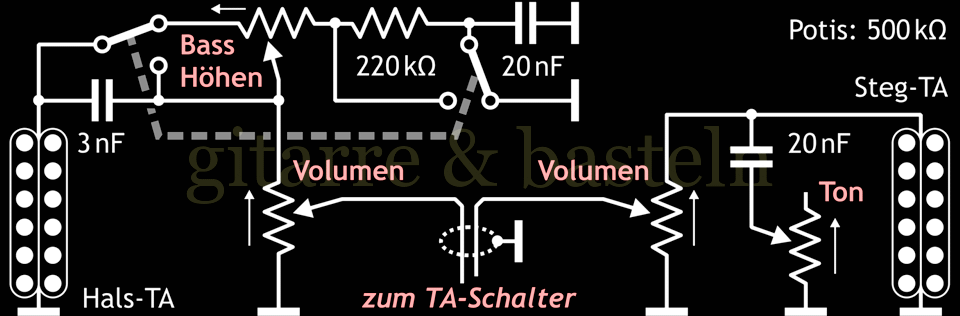
Abb. 6.10: Schaltungsvorschlag für einen umschaltbaren Bass-/Höhenregler für den Halstonabnehmer einer Les Paul (Schalter auf Stellung Bassregler).
Nachteil dieser Schaltung ist allerdings, dass das Potentiometer wahrscheinlich eine logarithmische Charakteristik hat, was für den Bassregler ein wenig ungünstig ist.
Aber irgendetwas ist ja immer …
Nun kurz zum mathematischen Hintergrund; begonnen wird mit der Formel für f1:
\( \begin{eqnarray} f_1 & = & \frac{1} { 2π\cdot{}C_{Bass}\cdot{}R_{Bass} } \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}003\cdot{}0{,}48 } \\~\\ f_1 & \approx{} & 110\,\textrm{Hz} \tag{6.15}\end{eqnarray} \)
f1 ist hier im Vergleich zu den Telecaster- und Stratocasterschaltungen ein wenig kleiner, weil der größere Bassregler (etwa 250 kΩ statt etwa 480 kΩ) durch die Verkleinerung des parallelgeschalteten Kondensators (etwa 4,7 nF statt etwa 3 nF) nicht vollständig ausgeglichen wird. Ähnliches gilt für f2:
\( \begin{eqnarray} f_2 & = & \frac{1} { 2π\cdot{}C_{Bass}\cdot{}\! \left( R_{Bass}\,||\,R_{Fuss}\,||\,R_{Vol}\,||\,R_{Ein} \right) } \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}003\cdot{}\! \left( 0{,}48\,||\,0{,}22\,||\,0{,}48\,||\,1 \right)} \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}003\cdot{}0{,}10 } \\~\\ f_2 & \approx{} & 510\,\textrm{Hz} \tag{6.16}\end{eqnarray} \)
Insgesamt ist die maximale Bassdämpfung vergleichbar groß:
\( \begin{eqnarray} D_{max} [\textrm{dB}] & = & 20\cdot{}\! \log \left( \frac{f_2} {f_1} \right) \\~\\ & = & 20\cdot{}\! \log \left( \frac{510\,\textrm{Hz}} {110\,\textrm{Hz}} \right) \\~\\ D_{max} & \approx & 13\,\textrm{dB} \tag{6.17}\end{eqnarray} \)
Wenigstens diese Schaltungsidee wurde auch praktisch umgesetzt – in der „Epiphone-Paula“ des Autors (siehe hier)
P. S: Les Paul – doppelter Klangregler
Die besten Ideen kommen häufig erst zu spät – zum Beispiel erschien die Idee eines linearen Zweiwege-Tonreglers für den Halstonabnehmer einer Les Paul mittels eines MN-Potentiometers (siehe die folgende Abbildung 6.11) erst, nachdem der Autor seine Epiphone mit einem Push-Pull-Potentiometer für einen kombinierten Klangregler neu verkabelt hatte.
Nicht destotrotz hier die neuere Idee:
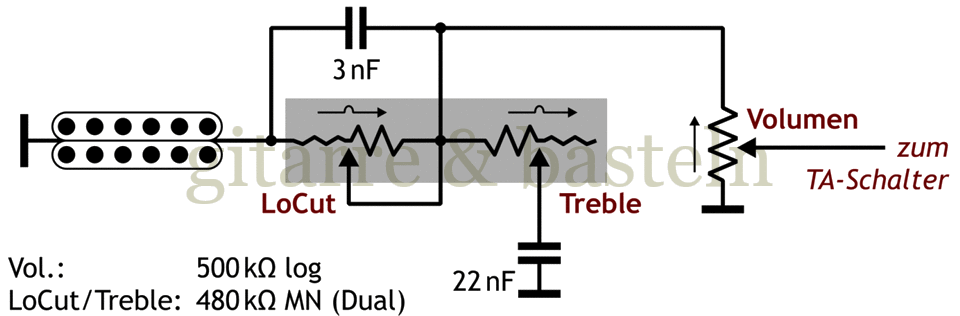
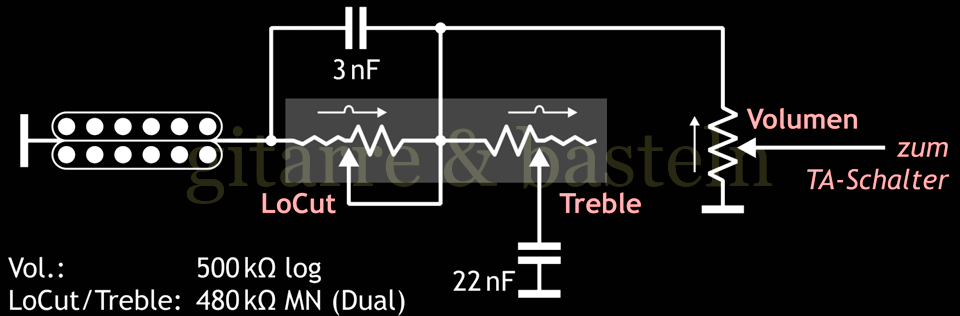
Abb. 6.11: Schaltungsvorschlag für einen Bass- Höhenregler in einer Les Paul – von dumpf (links) über neutral (Mitte) bis zur Bassabsenkung (rechts).
Der Klangregler bewegt sich (wie bei ganz alten Radios) von dumpf nach dünn, wobei die Einstellung in der Mitte einem voll aufgedrehten klassischem Tonregler entspricht.
Auch hier nun zum mathematischen Teil der Betrachtung – vor der Ableitung der maximalen Bassdämpfung zunächst die beiden Frequenzen f1 und f2. Für f1 ändert sich – bei gleichem Potentiometerwert und gleichem Kondensator – erst einmal nichts:
\( \begin{eqnarray} f_1 & = & \frac{1} { 2π\cdot{}C_{Bass}\cdot{}R_{Bass} } \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}003\cdot{}0{,}48 } \\~\\ f_1 & \approx{} & 110\,\textrm{Hz} \tag{6.18}\end{eqnarray} \)
f2 ist ein wenig kleiner,
\( \begin{eqnarray} f_2 & = & \frac{1} { 2π\cdot{}C_{Bass}\cdot{}\! \left( R_{Bass}\,||\,R_{Treble}\,||\,R_{Vol}\,||\,R_{Ein} \right) } \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}003\cdot{}\! \left( 0{,}48\,||\,0{,}48\,||\,0{,}5 \,||\,1 \right)} \\~\\ & = & \frac{1\,\textrm{Hz}} {2π\cdot{} 0{,}003\cdot{}0{,}14 } \\~\\ f_2 & \approx{} & 380\,\textrm{Hz} \tag{6.19}\end{eqnarray} \)
wodurch auch die Dämpfung im Bass geringer ist:
\( \begin{eqnarray} D_{max} [\textrm{dB}] & = & 20\cdot{}\! \log \left( \frac{f_2} {f_1} \right) \\~\\ & = & 20\cdot{}\! \log \left( \frac{380\,\textrm{Hz}} {110\,\textrm{Hz}} \right) \\~\\ D_{max} & \approx & 11\,\textrm{dB} \tag{6.20}\end{eqnarray} \)
Die mögliche maximale Bassdämpfung ergibt sich zu etwa 11 dB. Letztendlich führt hier der fehlende zusätzliche Fußwiderstand zu einem kleineren Wert von f2 und zu einer geringeren maximalen Bassdämpfung.
Fazit
Die von Jon Blackstone vorgeschlagenen Schaltungen arbeiten mit einem in vorgeschalteten und mit einem kleinen Kondensator überbrückten Potentiometer sowie einem dahinterliegenden Fußwiderstand gegen Masse. Mit diesem Arrangement sind ausreichend große Bassabsenkungen möglich, die durch den Fußwiderstand auch etwas sicherer sind gegen den Einfluss eines kleineren Eingangswiderstandes eines nachfolgenden Gerätes.
Wegen des geringen Fußwiderstands ist es also nicht ganz so wahrscheinlich, dass einem angeschlossenen Bodeneffektgerät hier ein „Soundverlust“ wie zum Beispiel eine „Mittennase“ angedichtet wird, weil sich durch einen Eingangswiderstand deutlich kleiner 1 MΩ die obere −3dB-Frequenz des Bassreglers deutlich nach oben verschiebt.
Die vom Autor vorgeschlagenen Schaltungen hingegen, wenn es sich nicht nur um einen Korrekturvorschlag (zur Telecaster, siehe hier) oder die Umschaltung des Tonreglers zum Bassregler über ein Push-Pull-Potentiometer (siehe hier) handelt, sollen lediglich ein wenig flexibler eingesetzt werden können; z. B. als kombinierter Bass-Höhen-Regler mit Nullstellung (siehe hier) oder als doppelter Bassregler für die Stratocaster (siehe hier).
Das heißt, beim Einsatz dieser Schaltungen vor einem Vintage-Effekt mit geringem Eingangswiderstand kann die Einstellung des Bassreglers schon ein wenig herausfordernd sein.
